Общие сведения о системах счисления
Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов свидетельствуют о том, что первоначально число предметов отображали равным количеством каких-либо значков (бирок): зарубков, чёрточек, точек. Такая система записи чисел называется единичной (унарной), т.к. любое число в ней образуется путём повторения одного знака, символизирующего единицу.
Унарная система – не самый удобный способ записи чисел: записывать таким образом большие значения утомительно, да и сами записи при этом получаются очень длинными. С течением времени возникли иные, более удобные и экономичные системы счисления.
Система счисления – это знаковая система, в которой числа записываются по определённым правилам с помощью символов некоторого алфавита, называемых цифрами. Количество цифр, составляющих алфавит, называется его размерностью или мощностью.
Различают непозиционные и позиционные системы счисления.
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от её положения в числе.
Примером непозиционной системы, которая сохранилась до наших дней – Римская система счисления.
В её основе лежали знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две скрещённые ладони) для числа 10, а для обозначения чисел 100, 500 и 1000 стали применять первые буквы соответствующих латинских слов (centum – сто, demimille – половина тысячи, mille – тысяча).
Чтобы записать число, римляне разлагали его на сумму тысяч (M), полутысяч (D), сотен (C), полусотен (L), десятков (X), пятёрок (V), единиц (I).
Например, десятичное число 128 представляется следующим образом:
CXXVIII = 100 + 10 + 10 + 5 + 1 + 1 + 1
(одна сотня, два десятка, пять, три единицы).
Для записи промежуточных чисел, римляне использовали не только сложение, но и вычитание. При этом применялось следующее правило: каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него.
Например, XI обозначает 11, а IX обозначает 9.
Римскими цифрами пользовались очень долго. Еще 200 лет назад в деловых бумагах числа должны были обозначаться римскими цифрами (считалось, что арабские цифры легко подделать). Римская система счисления сегодня используется в основном для наименования знаменательных дат, томов, разделов и глав в книгах.
Непозиционные системы счисления имеют ряд существенных недостатков:
- существует постоянная потребность введения новых знаков для записи больших чисел;
- невозможно представлять дробные и отрицательные числа;
- сложно выполнять арифметические операции, т.к. не существует алгоритмов их выполнения;
Всех перечисленных выше недостатков лишены позиционные системы счисления.
Например, используемая повсеместно десятичная система счисления – позиционная.
Рассмотрим число 555.
Цифра 5, стоящая в записи этого числа на первом месте, обозначает количество сотен и соответствует числу 500; цифра, стоящая посередине, обозначает 5 десятков (50); последняя цифра 5 соответствует пяти единицам. Исходное число можно представить в виде суммы: 555 = 500 + 50 + 5.
Позиционные системы счисления
Существует бесконечно много позиционных систем счисления. Каждая из них определяется целым числом q > 1, называемым основанием системы счисления. Основание определяет (даёт) название системы счисления: двоичная, троичная, восьмеричная, шестнадцатеричная, q-ичная и т.д. Можно говорить “система счисления с основанием q”.
Основное достоинство любой позиционной системы счисления – возможность записи произвольного числа ограниченным количеством символов. Для записи чисел в позиционной системе счисления с основанием q нужен алфавит из q цифр: 0, 1, 2, …, q – 1.

В q-ичной системе счисления q единиц какого-либо разряда образуют единицу следующего разряда.
Целое число без знака A в q-ичной системе счисления представляется в виде конечной суммы степеней числа q – суммы разрядных слагаемых:
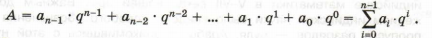
Здесь:
- q – основание системы счисления;
- ai – цифры, принадлежащие алфавиту данной системы счисления (0 ⩽ ai ⩽ q – 1);
- qi – весовой коэффициент разряда.
Последовательность чисел, каждое из которых задаёт “вес” соответствующего разряда, называется базисом позиционной системы счисления.
Свёрнутой формой записи числа мы пользуемся в повседневной жизни, иначе её называют естественной формой или цифровой.
Развёрнутая форма записи числа также хорошо всем известная. Ещё в начальной школе дети учатся записывать числа в виде суммы разрядных слагаемых.
Например:
125248 = 1 * 100000 + 2 * 10000 + 5 * 1000 + 2 * 100 + 4 * 10 + 8 * 1.
Если представить разряды в виде степей основания, то получим: 125248 = 1 * 105 + 2 * 104 + 5 * 103 + 2 * 102 + 4 * 101 + 8 * 100.
Аналогичным образом представляются и дроби:
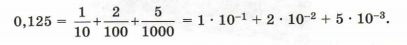
Перевод чисел из q-ичной в десятичную системы счисления
Перевод числа, записанного в системе счисления с основанием q, в десятичную систему счисления основан на использовании развёрнутой формы записи чисел.

Переведём числа 2123, 1235 и 12A16 в десятичную систему счисления:
2123 = 2 * 32 + 1 * 31 + 2 * 30 = 2 * 9 + 1 * 3 + 2 * 1 = 2310
1235 = 1 * 52 + 2 * 51 + 3 * 50 = 2 * 25 + 2 * 5 + 3 * 1 = 6310
12A16 = 1 * 162 + 2 * 161 + A * 160 = 1 * 256 + 2 * 16 + 10 * 1 = 29810
Перевод в десятичную систему счисления целых двоичных чисел будет значительно проще, если вспомнить и использовать уже знакомую вам таблицу степеней двойки:
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2n | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
Например:
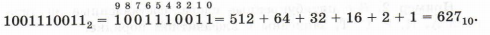
Для перевода двоичного числа в десятичную систему счисления можно воспользоваться схемой Горнера:
- 1 * 2 = 2 – возьмем 1, соответствующую самому старшему разряду числа, и умножим её на 2;
- 2 + 0 = 2 – прибавим следующую цифру;
- 2 * 2 = 4 – умножим результат на 2;
- 4 + 0 = 4 – прибавим следующую цифру;
- 4 + 2 = 8 – умножим результат на 2;
- 8 + 1 = 9 – прибавим следующую цифру;
- 9 * 2 = 18 – умножим результат на 2;
- 18 + 1 = 19 – прибавим следующую цифру;
- 19 * 2 = 38 – умножим результат на 2;
- 38 + 1 = 39 – прибавим следующую цифру;
- 39 * 2 = 78 – умножим результат на 2;
- 78 + 0 = 78 – прибавим следующую цифру;
- 78 * 2 = 156 – умножим результат на 2;
- 156 + 0 = 156 – прибавим следующую цифру;
- 156 * 2 = 312 – умножим результат на 2;
- 312 * 1 = 313 – прибавим следующую цифру;
- 313 * 2 = 626 – умножим результат на 2;
- 626 + 1 = 627 – прибавим последнюю цифру;
Решение задач
Задача 1.
Десятичное число 57 в некоторой системе счисления записывается как 212. Определим основание этой системы счисления.
Запишем условие задачи иначе: 212q = 5710, q > 2.
Представим в виде суммы разрядных слагаемых:
212q = 2 * q2 + 1 * q1 + 2 * q0 = 2q2 + q + 2 = 5710
Решим уравнение: 2q2 + q + 2 = 57 => 2q2 + q – 55 = 0
Это квадратное уравнение, его корни x1 = – 5,5; x2 = 5.
Так как основание системы счисления должно быть натуральным числом, то q = 5.
Задача 2
Все пятибуквенные слова, составленные из пяти букв А, И, Р, С, Т, записаны в алфавитном порядке.
Вот начало списка:
- ААААА
- ААААИ
- ААААР
- ААААС
- ААААТ
- АААИА
…
Необходимо найти ответы на два вопроса.
- На каком месте от начала списка стоит слово ИСТРА?
- Сколько всего слов в этом списке?
Введём следующие обозначений: А – 0, И – 1, Р – 2, С – 3, Т – 4. Перепишем в новых обозначениях исходный список:
- 00000
- 00001
- 00002
- 00003
- 00004
- 00010
…
Теперь перед нами последовательность чисел от 0 до 44444, записанных в пятеричной системе счисления. При этом на 1-м месте в этой последовательности находится 0, на 2-м месте – 1, на 3-м месте – 2 и т.д. Это значит, что само число на единицу меньше того места (номера), которое оно занимаем в последовательности. Представив слово ИСТРА в новых обозначениях, получим 134205.
Переведём это пятеричное число в десятичную систему счисления:
134205 = 1 * 54 + 3 * 53 + 4 * 52 + 2 * 51 + 0 * 50 = 625 + 375 + 100 + 10 = 111010.
Это число находится в списке на 1111-м месте.
Чтобы выяснить, сколько всего слов в списке, запишем его самое последнее слово: ТТТТТ.
Ему соответствует число 444445.
444445 = 4 * 54 + 4 * 53 + 4 * 52+ 4 * 51+ 4 * 50 = 312410.
В списке это число стоит на 3125-м месте.
Задача 3.
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 60, запись которых в четверичной системе счисления оканчивается на 31.
В четверичной системе счисления используются цифры 0, 1, 2 и 3; число представляется в виде суммы разрядных слагаемых:
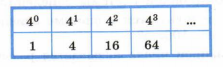
Из этой таблицы видно, что интересующие нас числа (⩽ 60) не будут более, чем трёхзначными.
С учётом того что их запись заканчивается на 31, определим первую цифру (k):
k * 16 + 3 * 4 + 1 ⩽ 60, k * 16 ⩽ 47, k ∈ {0, 1, 2}.
Искомые числа: 314 = 1310 (k = 0), 1314 = 2910 (k = 1), 2314 = 4210 (k = 2).
Источники: Босова Л. Л., Босова А. Ю., Информатика: учебник для 10 класса. М. : БИНОМ. Лаборатория знаний