Арифметические операции в позиционных системах счисления

Сложение чисел в системе счисления с основанием q

Арифметические операции в позиционных системах счисления с основанием q выполняются по правилам, аналогичным правилам, действующим в десятичной системе счисления.

В начальной школе для обучения детей счёту используют таблицы сложения и умножения. Подобные таблицы можно составить для любой позиционной системы счисления.

Рассмотрите ниже примеры таблиц сложения в троичной, восьмеричной и шестнадцатеричной системах счисления.

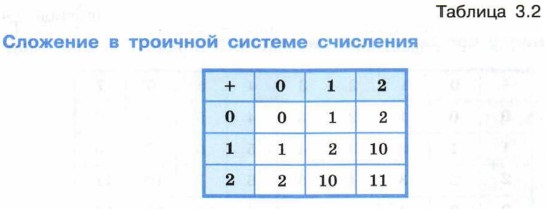
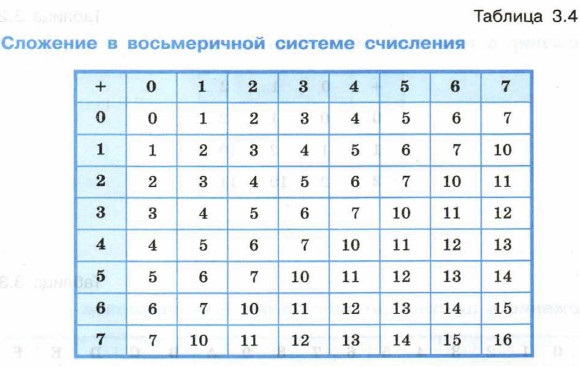
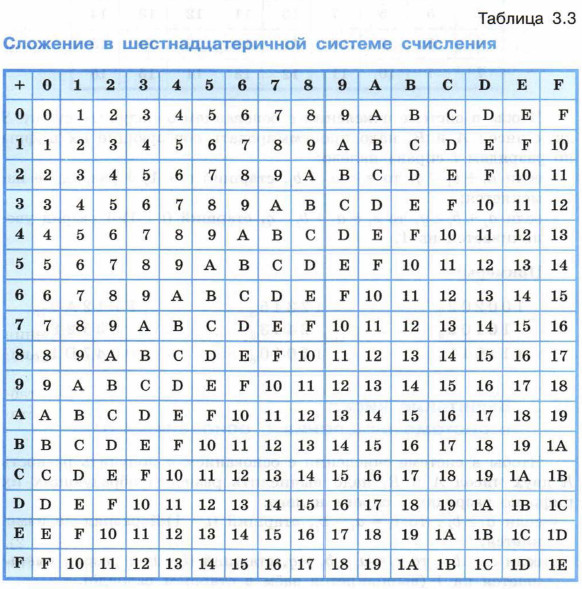
Чтобы в системе счисления с основанием q получить сумму S двух чисел А и В, надо просуммировать образующие их цифры по разрядам i справа налево:

• если а_i + b_i < q, то s_i = а_i + b_i, старший (i + 1)-й разряд не изменяется;
• если a_i + b_i ≥ q, то s_i = а_i + b_i– q, старший (i + 1)-й разряд увеличивается на 1.

Примеры:

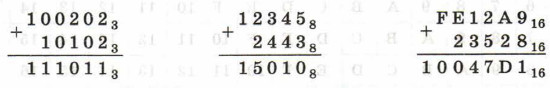
Вычитание чисел в системе счисления с основанием q

Чтобы в системе счисления с основанием q получить разность R двух чисел А и В, надо вычислить разности образующих их цифр по разрядам i справа налево:

• если a_i ≥ b_i , то г_i = а_i – b_i, старший (i + 1)-й разряд не изменяется;
• если a_i < b_i , то r_i = a_i – b_i + q, старший (i + 1)-й разряд уменьшается на 1 (выполняется заём в старшем разряде).

Примеры:

Умножение чисел в системе счисления с основанием q

Рассмотрите примеры таблиц умножения в троичной, восьмеричной и шестнадцатеричной системах счисления.

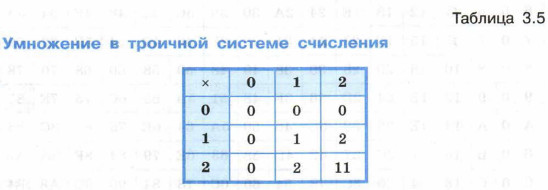
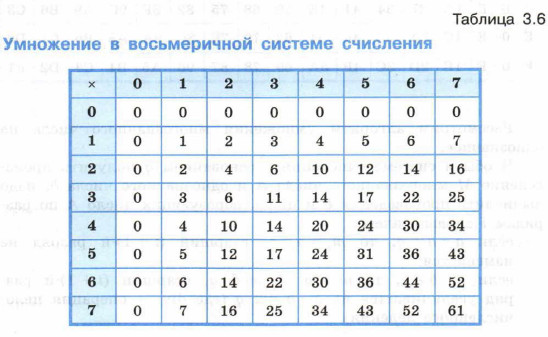
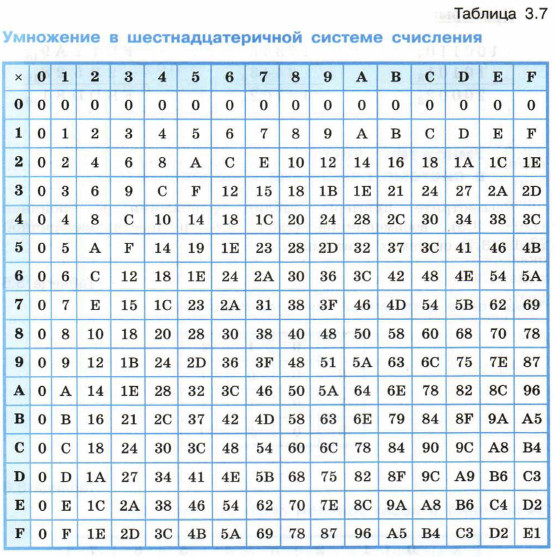
Рассмотрим алгоритм умножения многозначного числа на однозначное. Чтобы в системе счисления с основанием q получить произведение М многозначного числа А и однозначного числа b, надо вычислить произведения b и цифр, образующих число А по разрядам i справа налево:

• если a_i • b < q, то m_i = a_i • b, старший (i + 1)-й разряд не изменяется;
• если a_i • b ≥ q, то m_i = а_i • b mod q, старший (i + 1)-й разряд увеличивается на a_i • b div q (где div — операция целочисленного деления).

Примеры:

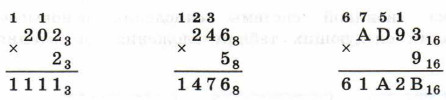
Умножение многозначного числа на многозначное число выполняется столбиком. При этом два множителя располагаются один под другим так, чтобы разряды чисел совпадали (находились в одном столбце).

Если один из множителей или оба множителя оканчиваются нулями, то числа записываются так, чтобы в одном столбце оказались их самые младшие разряды с цифрами, отличными от нуля. Нули переносятся в итоговое произведение, а в поле записи поэтапных произведений не заносятся.

Поэтапные (разрядные) произведения складываются по разрядам и под чертой записывается результат.

Примеры:

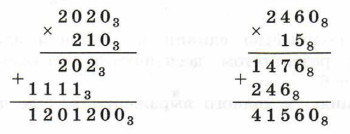
Деление чисел в системе счисления с основанием q

Деление нельзя свести к поразрядным операциям над цифрами, составляющими число.

Деление чисел в системе счисления с произвольным основанием q выполняется так же, как и в десятичной системе счисления.

Пример:

Двоичная арифметика

Арифметика двоичной системы счисления основывается на использовании следующих таблиц сложения, вычитания и умножения:

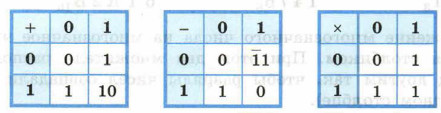
Рассмотрим несколько простых, но очень важных примеров на сложение и вычитание в двоичной системе счисления.

Примеры:

Пример 1.

Найдём количество единиц в двоичной записи числа, являющегося результатом десятичного выражения

2⁴⁰⁰⁰ + 4²⁰¹⁶ + 2²⁰¹⁸ – 8⁶⁰⁰ + 6.

Представим все операнды исходного выражения в виде степеней двойки:

4²⁰¹⁶ = (2 • 2)²⁰¹⁶ = (2²)²⁰¹⁶ = 2^{2 • 2016} = 2⁴⁰³²
8⁶⁰⁰ = (2³)⁶⁰⁰ = 2¹⁸⁰⁰
6 = 4 + 2 = 2² + 2¹

Исходное выражение примет вид:

2⁴⁰⁰⁰ + 4²⁰¹⁶ + 2²⁰¹⁸ – 8⁶⁰⁰ + 6 = 2⁴⁰⁰⁰ + 2⁴⁰³² + 2²⁰¹⁸ – 2¹⁸⁰⁰ + 2² + 2¹.

Перепишем выражение в порядке убывания степеней:

2⁴⁰³² + 2⁴⁰⁰⁰ + 2²⁰¹⁸ – 2¹⁸⁰⁰ + 2² + 2¹.

Для работы с десятичными числами вида 2ⁿ полезно иметь в виду следующие закономерности в их двоичной записи:

2¹ = 10 = 1 + 1;
2² = 100 = 11 + 1;
2³ = 1000 = 111 + 1;
2⁴ = 10000 = 1111 + 1 и т. д.

В общем виде:

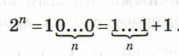
Для натуральных n и m таких, что n > m, получаем:

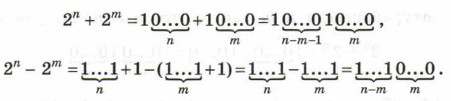
Эти соотношения позволят нам подсчитать количество единиц в нашем выражении, не прибегая к его вычислению.

Действительно, двоичные представления чисел 2⁴⁰³² и 2⁴⁰⁰⁰ внесут в двоичное представление суммы по одной единице.

Разность 2²⁰¹⁸ – 2¹⁸⁰⁰ в двоичной записи представляет собой цепочку из 218 единиц и следующих за ними 1800 нулей.

Слагаемые 2² и 2¹ дают ещё 2 единицы.

Итого: 1 + 1 + 218 + 1 + 1 = 222.

Пример 2

Найдём количество цифр в восьмеричной записи числа, являющегося результатом десятичного выражения

Двоичное представление исходного числа имеет вид:

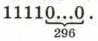
Всего в этой записи 300 двоичных символов.

При переводе двоичного числа в восьмеричную систему счисления каждая триада исходного числа заменяется восьмеричной цифрой. Следовательно, восьмеричное представление исходного числа состоит из 100 цифр.

Источники: Босова Л. Л., Босова А. Ю., Информатика: учебник для 8 класса. М. : БИНОМ. Лаборатория знаний